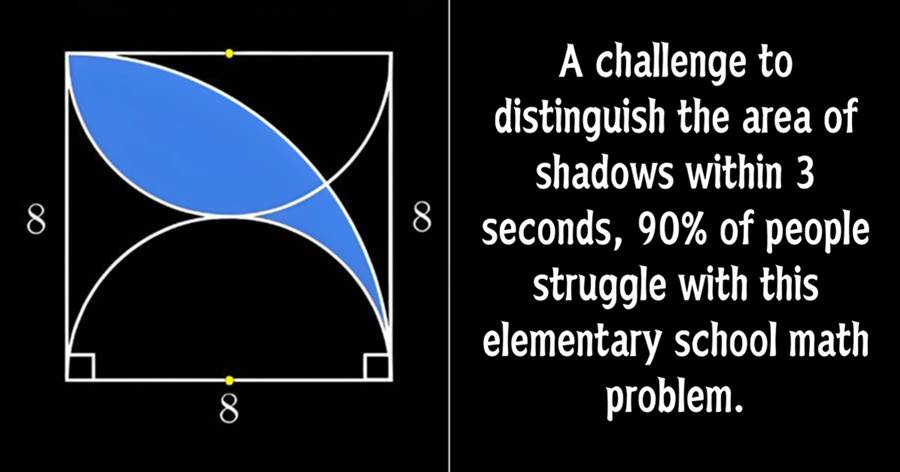
Recently, I brushed up on a geometry problem, staring at the shadow in the shape of a blue leaf, remembering the scratching of my ears and cheeks when I used to learn the area, but now I actually have an idea at a glance, and I can't help but want to nag.

It's a square with 8 sides and a shadow surrounded by curves. In the past, when I encountered this kind of problem, I would only calculate the area of the fan and triangle, but now I have a different way of thinking: divide and translate the figure.

Looking at this shadow, we can actually find that it is equivalent to a quarter circle with a radius of 8, minus the area of an isosceles right triangle with a right angle of 8.

The square area is 8×8=64, and half is 32. So the shadow area is 32.

The principle is like putting together a tangram, reorganizing the scattered parts, and the complex problem becomes simple in an instant.

This question reminds me of playing puzzles when I was a child, and finding the right method will do more with less. Are you right? Talk about your thoughts in the comment area~